Qubit能吃嗎?

2019-01-15
這幾天,各大科技網站都在報道IBM展示了世界上第一部商用的量子電腦, 不少科技網站也將量子計算形容為最期待的未來科技。那到底量子計算是何方神聖?為何令大家都引頸以待呢? 要理解量子計算的基本原理,最佳方法,就是由傳統的位元(bit)談起。

IBM Q System One
Source:https://www.pcgamesn.com/ibm-integrated-quantum-computer
位元(Bit)
電腦的最基本運算單位(Unit of information)就是一個位元(bit),八個位元就組成了常用的位元組(byte)。在電腦中,要代表一個位元,為簡單起 見,可以用一個晶體管(Transistor)去理解:

Source: Wikipedia
晶體管的原理,在於利用 Voltage(圖中的Vin)提供基極電壓,去控制通電與否。因此晶體管可以作為電源開關使用。有了這個電源開關的概念,例如 使用通電(Vcc 及 Vout)作為1,不通電(Vcc 及 Vout)作為0,就能夠表示一個位元的概念,再以此作基礎,建造不同的邏輯閘,就能夠造出能計算布爾、 (Boolean)代數的機器,現代電腦亦由千千萬萬的晶體管所組成。

Source: Wikipedia
以上是一個And Gate的具體呈現,只有當A及B都有施加基極電壓時,(V 及 Out)才會通電,這正正如就邏輯學中的 A & B的運作模式。
作看之下,AND Gate很簡單,看看XOR Gate(也就是僅 A 及 B都不同時才會是真值,一樣的時候,不論A及B本身真假,永遠是假值)的結構,
就遠複雜得多。

Source: Wikipedia
由以上例子可見,位元由晶體管表達這個概念是現代電腦的基礎,由1947年發明晶體管以來深遠地改變了人類的科技發展。
順帶一提,大家可能聽聞過CPU有發展極限,也就是CPU的速度只能快到一定程度,正正是由於晶體管的結構,當CPU的速度要求愈快,晶體管的大小也愈小, 因此量子效應(Quantum Effect)就會愈大,當晶體管小到一定程度,會出現一種叫量子隧道效應(Quantum Tunneling)的現象,令晶體管不論 有否基極電壓,皆在通電狀態,就會令晶體管作為電源開關的作用失效了。因此就失去了運算能力。 因為,晶體管的結構只有兩個有效狀態:通電(1)與不通電(0),也就是傳統電腦位元的兩個狀態。
量子位元(Qubit)
量子位元與位元非常不同,要理解量子位元,要先理解何謂量子態(Quantum State),正如我們的位元也有兩個狀態,量子位元的量子態也就是該量子位元所在狀態。與傳統電腦位元必須處於其中一個狀態不同,量子位元可以同時處於兩個狀態,這種現象稱為量子疊加 (Quantum Superposition)。 想容易理解這種奇怪現象,可以用下圖稱為Bloch Sphere的圖表去理解:

Source:Wikipedia
大家可以想像上圖是一個氣球,而一個位元是一隻螞蟻。對傳統位元螞蟻來說,牠只能在 北極點(|0>)或是 南極點(|1>):未通電前,牠在北極點(|0>); 通電後,牠在南極點(|1>)。量子位元螞蟻則不同,牠可以處於球面上任何一點,當然牠也可以停留在北極點或南極點,但於牠而言,這只是特例。 可以停留在球面上任何一點又代表甚麼?代表對量子位元螞蟻來說,牠有一定概率在北極點,也有一定概率在南極點。
你可能會想,這不簡單嗎?我們只要量度一下,量子位元螞蟻在那裏不就一目了然?沒這麼簡單,當我們嘗試量度量子位元螞蟻時,我只會得到北極點或是南 極點,這種效應又是一種量子現象,稱為波函數塌縮(Wave function collapse),也就是量度後量子位元螞蟻再不是有一定概率在南北極點,而是 一定在北極點、南極點其中一點。
而重要的是,正正是我們的量度,令量子位元螞蟻的波函數塌縮,也就是量度本身,就已經改變了量子位元螞蟻。
很頭昏腦漲是嗎?這很正常,正如1922諾貝爾物理學獎得主波爾(Niels Bohr)所言:
Anyone who is not shocked by quantum theory has not understood it.
- Niels Bohr
量子位元的優勢
量子位元很奇怪就是了,那比起傳統位元有何優勢?其實與剛才量子位元螞蟻及傳統位元螞蟻有莫大關係,因為傳統位元只要一個0或是1就可以表達其狀態。 但量子位元則可以在Bloch Sphere上任何一點,所以多出了兩個自由度(Degree of Freedoms),所謂自由度,就是在統計中能獨立變化的參數。 想像一下,一個相加函數:
function sum(a:number,b:number){ return a +b; }
這個函數就可以稱為有兩個自由度。同樣要表達量子位元也多出了兩個自由度,也就是上圖的兩個角度θ及 φ。 多出了兩個角度,代表同樣一個位元,量子位元所包含的資訊遠比傳統位元要多得多。 一個有n個傳統位元的系統顧名思義可以表示n bits的資訊,但有n個量子位元的系統則需要 (2^n -1) 個複數才能表達。
多倍的狀態,代表多個量子位元所能組成的複雜程度將遠超傳統電腦,正是這個原因,科學界才對量子計算寄以厚望。
現今進程
不同的科技公司,Google、 IBM、 Microsoft等都在積極研究,建設可供大眾使用的電腦。為何普通電腦無法使用量子位元呢? 因為上段所提的現象,都是量子現象。量子現象在我們日常生活的世界基本上不起作用,大家總不會真的看見一隻螞蟻又出 現在南極又出現在北極。只有在觀察微觀世界(Microscopic World)時,量子現象才會變得顯著。而大部份科技公司所研究的,是使用超導體作為 代表量子位元的元件,因為在超低溫(-70C以下),不同材料在不同溫度會呈現超導現象,也就是電阻變為零,而在這狀態下,電子的量 子效應亦會得非常突出,因此就能用作量子位元了。
還有許多不同的實現,科學家也正在努力研究,可能有朝一日,會有常溫量子電腦的出現吧。
總結
談了這麼多物理學,作為程式設計師的我們可以如何參與?就是可以嘗試一下IBM推出的量子計算框架Qiskit,一起感受 一下量子力學的吊詭,體驗未來的編程。
留言
閱讀更多
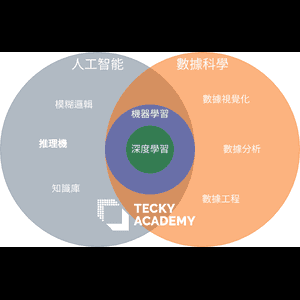
Data Science? AI ? Machine Learning? 到底有何分別?

2018-11-23
近幾年大家經常聽到 Data Science(數據科學)、AI(人工智能)、Machine Learning(機器學習)、 Deep Learning(深度學習)等等詞彙, 以上的名詞的意思好像差不多,但又並非完全一樣

資訊熵

2018-12-18
資訊量有方法量度嗎?當然有,一句十個字訊息跟一百字訊息所包含的資訊當然大相逕庭。光看字數準確嗎?同一語言還可,然而不同語言不同字數所表達的 意思不同,本身根本不可比。看檔案大小可以嗎?有時可以有時不可以,因為不同檔案類型大小不同,光看檔案大小並不準確。 因此,電腦科學中有一個數學方式表達資訊量,此概念就是資訊熵(Information Entropy)。
馮紐曼

2018-12-28
今日是12月28日,115年前的今日,一位對現今電腦有深遠影響的天才出世了。他一生對數學、電腦科學、物理學貢獻良多,被譽為電腦科學其 中一位奠基人,與廣為人所知的艾倫‧圖靈齊名,他就是約翰‧ 馮紐曼(John von Neumann)。